News

Elliptical curves

An address on the bitcoin network – for example, 1HGY3FhkXAZkBQUaW2syrWtRreFiXSmE1y is actually a string derived from the ECDSA public key. ECDSA is an asymmetric digital signature algorithm from the Elliptic Curve Cryptography (ECC) family. As with RSA or DSA, for example, there is a private-public key pair in ECDSA. RSA relies on the mathematical complexity of factoring extremely high numbers, i.e., decomposing a number into the product of two primes. In contrast, ECC relies on the algebra of elliptic curves, in particular group operations over them.

The basic advantage of elliptic curves is their economy of notation. Theory suggests that with ECDSA key lengths of 256 bits, roughly the same complexity as RSA 2048 bits can be achieved. Another advantage of ECDSA is slightly faster key generation or signing operations. On the other hand, the disadvantage (and vice versa point for RSA or DSA) is that ECC technology is relatively young. For the more conservative part of the enterprise segment, this is probably a reason to wait to deploy it. Doubts have surfaced following reports of possible compromise of the ECC algorithm by the US NSA through manipulation of the random number generator. However, it should be added here that by implementing ECC correctly, the problem can be eliminated.

Let us illustrate the basic advantage of ECDSA over RSA. Below are examples of different public keys generated by Puttygen for SSH authentication.

First the most widely used RSA/2048:

ssh-rsa AAAAB3NzaC1yc2EAAAABJQAAAQEAhkkj6rIOvaUxlEk0Mel3icHvArD8LpuwT2fp8t8WZEVPPieIC48wxlOmr7LulMogQl1VFfJEL K+RkE1jH4kIoxlJdhqAw5xQsIN6wQ+YAG5HaFqz6jvWdrRTijZSZu2wLKKHz7wHt84yBmLg4TemGBqzI4e001WltaLik9tZEj265RY viHha7+QUUIBPuZby5znLdLgEy7W0+qq7hll9yl+eG1d/kTKr6lnm4zb9E7OKSHfdCxkfGDvU68sc2SNahJ9Myp8EjnfpFX7KEplLJV B0sKOmBZdyCyUG37YKZWtaxXGq8FphDTBiepAe1/GZgYVWCbDqlgCfSo9vO+p/fQ==

Using ECC/256 is a big saving:

ecdsa-sha2-nistp256 AAAAE2VjZHNhLXNoYTItbmlzdHAyNTYAAAAIbmlzdHAyNTYAAABBBPaMGrNfyeNupUShdrRF7cJNGzIad2Go/c7iFNpPaSLxB42 HVVHYYMiXGt/fBo8M8+OrVTCtttzbu+L5Q9izQEw=

The shortest writes can be achieved using the ED25519 variant (again 256 bit):

ssh-ed25519 AAAAC3NzaC1lZDI1NTE5AAAAIHbXGFH+YepmWiNx78aisGyAShocV+7F5RLUTY5HRZWz

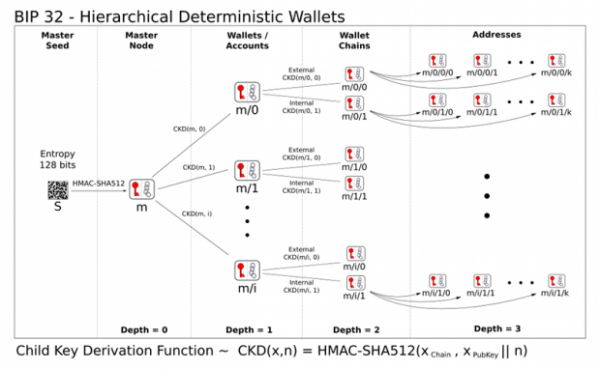
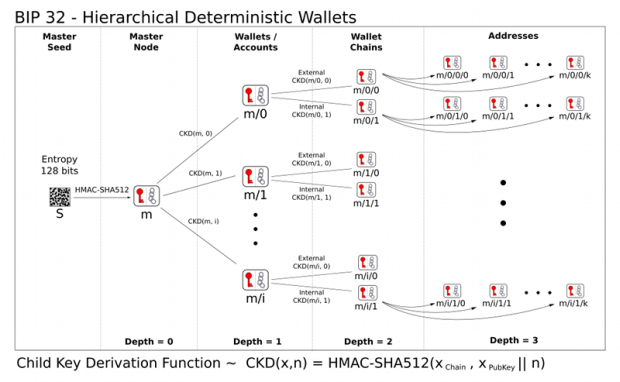
Deterministic hierarchy

This term hides a different approach to asymmetric key generation than most of us are probably used to. Classical asymmetric key generation (e.g. RSA or ECDSA) is done by generating one private-public key pair. That is, there is one public key associated with one private key. The reverse is also true, one private key belongs to one public key.

In the Bitcoin world, such a private key is actually a wallet. Simply put, whoever has a private key (wallet) to a public key (address) can spend the Bitcoins that belong to that address. In the Bitcoin network, it is common for users to have many addresses generated – tens or even thousands. For each address, the user must keep a private key. Users should back up their keys because if they lose them, they will lose their bitcoins and there is no (at least I hope 🙂 force in the world that can change that. In practice, this means that the more addresses I generate, the more often I have to back them up.

Finally, I come to an explanation of the deterministic hierarchy (wallet) technology that was added to the Bitcoin protocol some time ago. The idea is that all keys and addresses are generated from a single initial secret – the so-called seed. The seed is typically created based on input from the user (for example, 12-24 words) and then more and more keys are deterministically derived from it. The number of keys derivable in this way specifically in the Bitcoin address space is almost unlimited and cannot realistically be exhausted in a human lifetime. A huge advantage of the hierarchical approach to key generation is the practicality of backup. Just write down a relatively short initial seed somewhere once (e.g., on a piece of paper stored in a vault) and it is possible to derive the entire wallet structure from it again.

Deterministic hierarchy has other advantages than backup. Just as all private keys are derived from an initial seed – in effect, a super private key, there is also a super public key. It is sometimes called XPUB. From this XPUB key, as you might guess, all possible public keys for a given hierarchy can be derived. If I choose to make the XPUB public, I allow someone else to keep track of all my bitcoin transactions. But without the ability to do the transactions themselves. A deterministic hierarchy forms a graph that can have different depths. The leaves of the tree are the keys (wallets), the inner nodes represent the data from which all the followers below can be inferred. In a tree, all elements except the vertex have exactly one direct ancestor. Other uses are straightforward. For example, if such a “tree” wallet were to work in a company, the CEO might have the master key and his subordinates might have only the keys in the specified hierarchy for which they are responsible.

Author: Martin Lízner works at AMI Praha as a solution architect and identity management specialist.